On Computation and Reinforcement Learning

The standard view in reinforcement learning (RL) is to treat RL policies as static functions that map states to actions. Policies typically spend a fixed amount of compute, regardless of the complexity of making the correct decision in the underlying state. For example, for a humanoid robot, the action of where to move the right foot is easy, but figuring out how to efficiently pack furniture in a truck requires more deliberation. In RL, this limitation is often solved by citing Moore's law and simply scaling the number of policy parameters. But the compute required to make good decisions in different situations can span many orders of magnitude; using a static massive policy with a large number of parameters is wasteful. Additionally, as compute becomes cheap, the complexity of the world and sensory data also increase, making it infeasible to simply scale up policy parameters.

The main contributions of our work are:

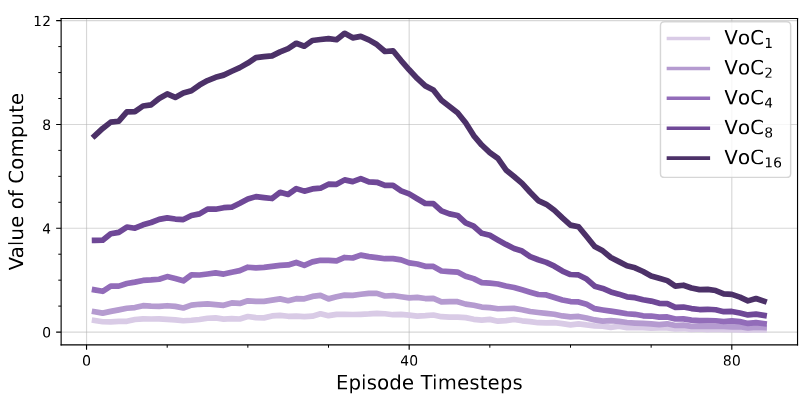
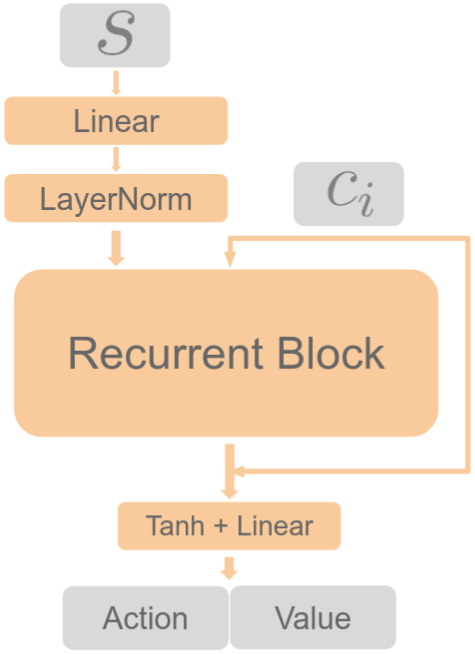
• We advocate for a computational view of RL, where computation time and parameter count are distinct axes. We formulate RL policies as bounded models of computation and prove that policies with more compute time can achieve arbitrarily better performance and generalization to longer horizon tasks depending on the MDP.
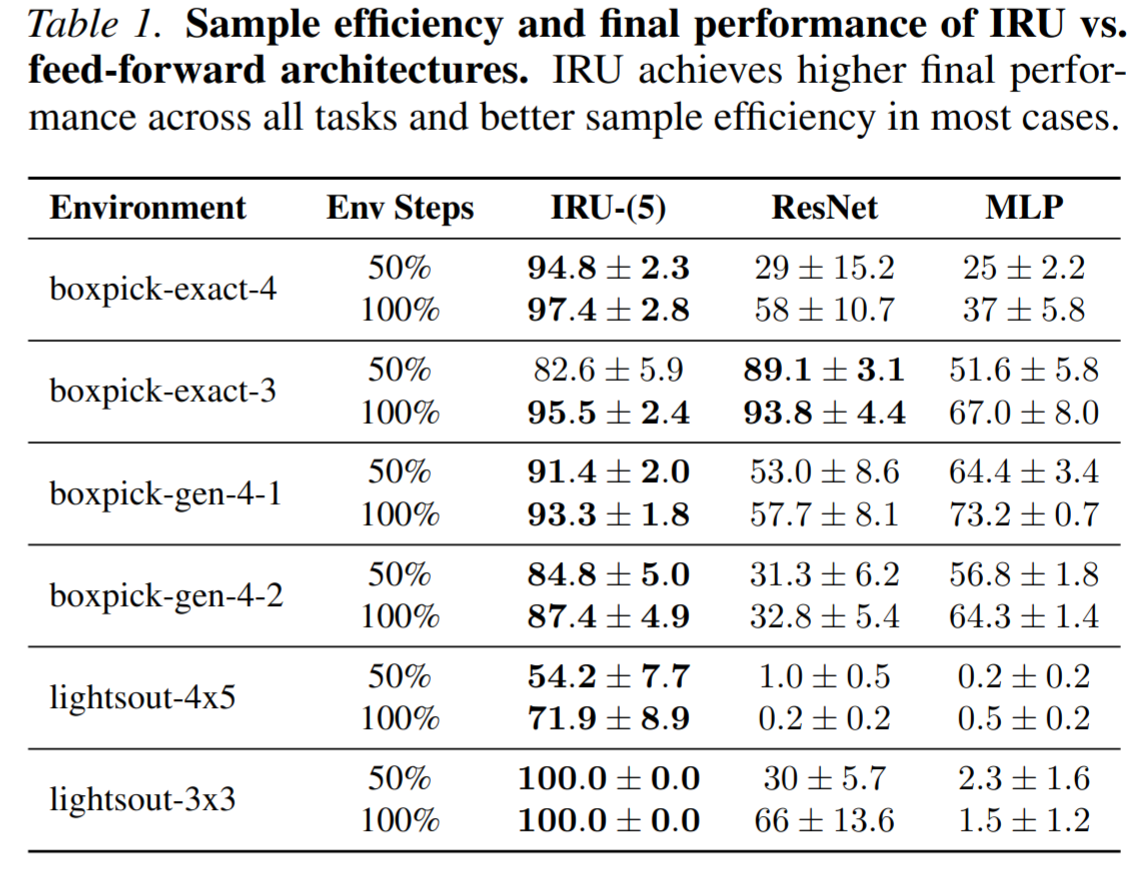
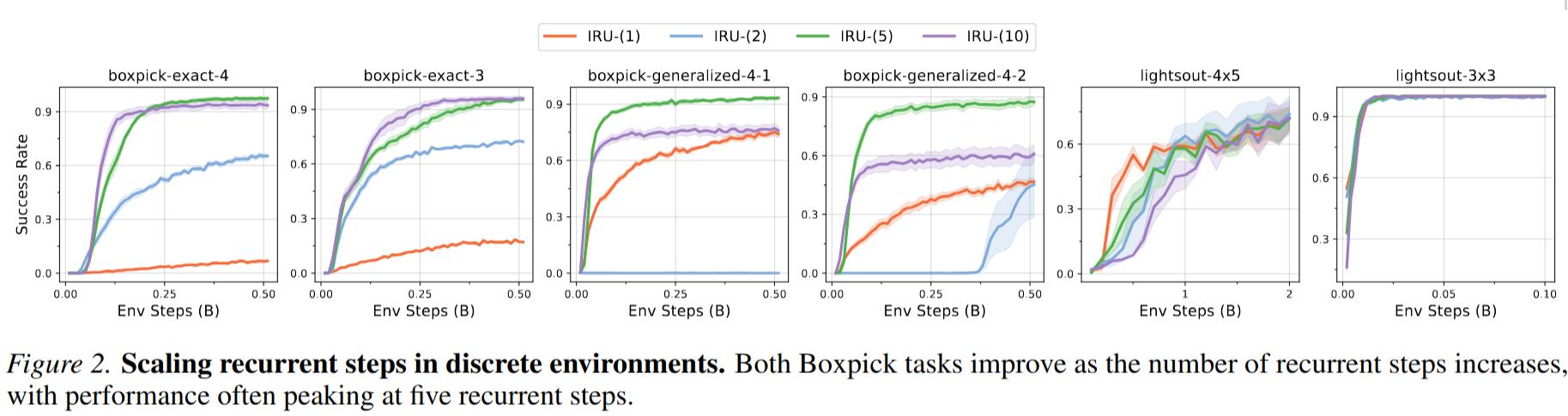
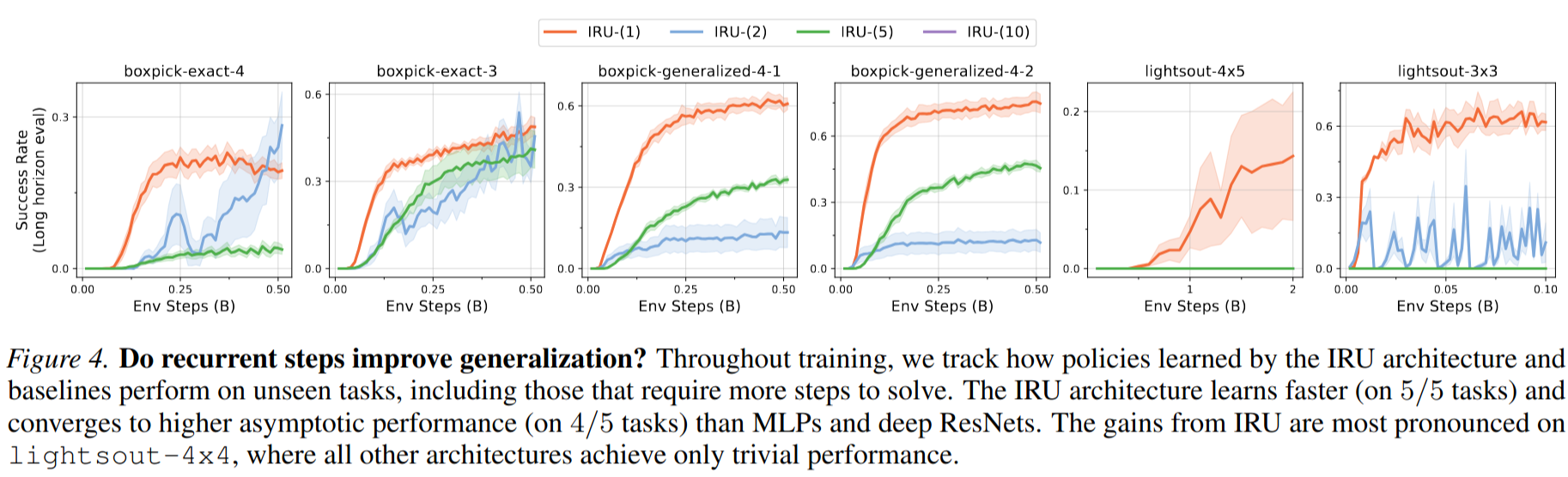
• We empirically show that RL policies which use more compute achieve stronger performance as well as stronger generalization to longer-horizon unseen tasks

In our experiments, we will use the above architecture for policy and value networks. These networks will take as input the observation and (for Q-functions) the action. After an initial Linear layer and Layer-normalization layer, we apply a recurrent block layer N times. After each application of the recurrent block, the previous cell state is added to the output using a skip connection. The final cell state, after a Tanh activation, is passed through a final linear layer to predict the actions and values. The entire architecture is referred to as IRU-(N).

To evaluate the proposed architecture across a wide range of tasks — including discrete and continuous — we conduct experiments in the following domains: boxpick stitching benchmark, lightsout puzzle and OGBench. The boxpick stitching tasks are difficult for RL algorithms, and many state of the art algorithms only achieve trivial performance on them. In the lightsout tasks, the space of possible inputs is very large (2²¹ for lightsout-4x5), hence it is challenging to memorize all the optimal actions.

On all discrete tasks we train on shorter horizon goals and evaluate on both shorter and longer horizon goals.

In the above table, we compare IRU-(5), with the MLP and the ResNet architecture after 2.5 (50%) and 5 (50%) million environment steps. On all tasks, IRU-(5) outperforms the MLP, which uses less compute but similar number of parameters. Notably, IRU-(5) is able to solve the most challenging tasks like boxpick-exact-4, boxpick-gen-4-1 and lightsout-4x5, achieving a significant performance boost over the ResNet architecture. This is despite the ResNet using ~2 times more compute and ~5 times more parameters than IRU-(5). We hypothesize that this is due to the ResNet overfitting to seen tasks. This hypothesis is supported by the higher standard error values for the ResNet architecture in.

In most of the discrete and continuous tasks, we see that performance increases significantly with more recurrent steps. In the challenging boxpick tasks, or the manipulation tasks in ogbench, performance increases up to 8 times after increasing the recurrent steps from one to ten.

Below we present an outline and intuition for our theoretical results. Please check our paper for formal statements, assumptions and proof.

The above theorem tells us that there exist tasks on which policy classes that have more compute perform arbitrarily better than policies with less compute. See our paper for the proof, which uses the time hierarchy theorems to construct the desired MDP. This result is interesting because it suggests that, under computational constraints, standard results about MDPs may no longer hold. For example, computation constraints may be reflected as partial observability, potentially explaining why prior experimental work has used non-Markov policies for solving ``fully observed'' tasks. While recent work has argued that additional computation ("thinking" or "reasoning") is primarily useful because it enables policies to leverage multi-task pre-training, this theorem shows that the value of additional computation does not depend on multitask learning nor on pre-training.

Importantly, additional computation need not translate to larger hypotheses classes with weaker generalization. Rather, policies that use additional compute can provably exhibit stronger generalization. The intuition, which we formalize in the next theorem, is that a certain amount of compute capacity is required to represent the correct algorithm, and compute-constrained models will instead learn heuristics.

The above theorem implies that a policy class with less compute can overfit on the training tasks of a more difficult problem and fail to generalize to longer-horizon tasks during evaluation. A simple example of this is language models being unable to solve GSM8K problems in a single forward pass (constant compute), but solving them when provided with more compute using chain of thought.

One limitation of our work is that we use a fixed amount of recurrent computation steps for all states. We do not demonstrate how the same policy can use an adaptive amount of compute depending on the difficulty of the current state. Future work could explore such methods which might automatically learn inference-time compute scaling strategies or pre-fetch anticipated computation to store in memory. Additionally, our empirical evaluation focuses on a minimal recurrent architecture to isolate the effects of computation. We do not explore transformer-based architectures, and given their ubiquity in machine learning, an exploration of transformer-based recursive architectures in RL remains an interesting direction for future research. Lastly, our theoretical results use a single tape Turing machine as a computational model and only focus on time-complexity. Similar interesting results could be proven for space complexity or by using computational models like boolean circuits which better resemble modern neural networks.